How Proof-of-Work… Works
 A Proof-of-Work system requires its users to perform some form of work to participate. The work must be difficult for the client but easy for the server/network to verify. For example, an email system that implements proof-of-work might require each sender’s computer perform 1-2 seconds of work before sending an email. Deployed this way helps prevent spam.
A Proof-of-Work system requires its users to perform some form of work to participate. The work must be difficult for the client but easy for the server/network to verify. For example, an email system that implements proof-of-work might require each sender’s computer perform 1-2 seconds of work before sending an email. Deployed this way helps prevent spam.
With Bitcoin, the POW also determines the approximate time between blocks and thus the rate that new bitcoins are created.
Also read: Bitcoin Mining Difficulty Decreases for First Time in Almost Two Years
Proof-of-Work
The code posted below is little more than a guessing game for the computer. The work it submits is a message/timestamp payload and a nonce value. Ideally your payload would be unique to you, perhaps using a public key or address. The nonce is what allows the network to check your work without retracing all of your steps. This code is little more than an example – based on my experience with BitMessage’s source code.
#!/bin/python
#Simple Proof-of-Work example
import sys
import time
import hashlib
from struct import unpack, pack
timestamp = str(time.time())
message = "This is a random message."
nonce = 0
guess = 99999999999999999999
payload = timestamp + message
throttle = 10000000
target = 2**64 / throttle
payloadHash = hashlib.sha512(payload).digest()
start = time.time()
while guess > target:
nonce += 1
guess, = unpack('>Q',hashlib.sha512(hashlib.sha512(pack('>Q',nonce) + payloadHash).digest()).digest()[0:8])
end = time.time()
print "%s:%s:%s:%s:%s:%s:%s" % (timestamp, message, nonce, guess, payload, target, end-start)
timestamp = str(time.time()) message = "This is a random message." nonce = 0 guess = 99999999999999999999 payload = timestamp + message throttle = 10000000 target = 2**64 / throttle
- timestamp marks the point that the work started. Additionally, it contributes to the uniqueness of the work by an individual miner.
- message is there because this code just for example. Hashing a string is suitable work for this project.
- payload is a combination of the things that you will encrypt.
- nonce will increment from 0..N until the target is met.
- guess will store our guess. Effectively, it begins at infinity.
- throttle is equivalent to Bitcoin difficulty.
- target is the maximum value of 8 bytes (2^64) divided by the difficulty.
The timestamp, message and payload are just the “stuff” that you want to send the network. It could be block data, as with Bitcoin mining.
The nonce, guess, throttle and target are used to perform the work. The important thing about proof-of-work is that it has to be difficult for the client but easy for the system to check. Only the nonce changes with each guess. The probability of being correct is so low that this system, probabilistically, guarantees many guesses or work, is performed.
In this example, nonce increments by 1 each time. Effectively counting how many guesses the computer makes. However, that is not a requirement.
When the system checks the work, it does not have to trace back over each guess. It only checks the nonce submitted with the data.
The Proof-of-Work Guessing Game
while guess > target:
nonce += 1
guess, = unpack('>Q',hashlib.sha512(hashlib.sha512(pack('>Q',nonce) + payloadHash).digest()).digest()[0:8])
These three lines are our proof-of-work algorithm. It’s a simple loop. This hashes our data with two rounds of SHA256. The first 8 bytes are turned in to a number. Effectively, this is how a computer makes a guess.
The target is calculated based on estimates I made with a little math and some trials in a smaller script I wrote to get an estimate of my CPU hash rate. I used this to determine a baseline of metrics to test the script on my computer. Here is the source
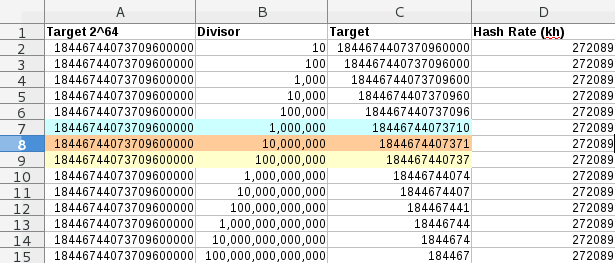
Bitcoin’s divisor is incremented or decremented after every correct 2016 guesses (every 2016 blocks are mined). This script does not recalculate difficulty. It is set manually. The image above shows how an increase in difficulty shrinks the target range lowering the possible number of correct guesses.
nonce += 1
The nonce is what proves the work was done. In this example, it’s value represents the number of attempts your CPU made before it found a valid guess below the target. Because each guess has the same probability of being under the target the method of generating your nonce does not matter. However, simply incrementing the nonce is cheaper than generating a random number. When work is submitted to the network, the nonce is used to verify the correctness.
guess, = unpack('>Q',hashlib.sha512(hashlib.sha512(pack('>Q',nonce) + payloadHash).digest()).digest()[0:8])
The actual guess is the first eight bytes of a double SHA512 hash of the nonce and the payload. Because the target is between 0 and the maximum eight byte number, a guess can never go over the maximum possible target value. In each loop, the nonce is the only thing that changes. That is what allows you to submit your unique work to the network and have it verified without each node duplicating all of your work. Giving them the nonce gives them the answer. With Bitcoin, theoretically every miner would submit a similar block to the network regardless of who made a the correct guess. The most significant difference to the miner would be their public key in the coinbase entitling them to the block reward.
Giving the network your nonce is secure because each miner’s payload, and therefore work, is unique. For Miner Alice to use the correct nonce that Miner Bob submits, Alice would have to submit the same work. Alice would not be able to switch out her public key with Bob’s in the coinbase (not the company Coinbase) because it would change the output from the double SHA512 hash – which would likely not be a correct guess with Bob’s nonce. In this example, no unique ownership can be assigned to the work. Any number of nodes doing this work with the same values for time and payload will do the same work. Perhaps said this way simply, Alice’s payload would differ from Bob’s payload making any nonce Alice, or Bob uses useless for the other’s work.
Testing the Proof-of-Work script
The three highlighted rows represented difficulties I considered reasonable for testing. These columns are a continuation of the image above. The Chance to Guess is the total possible correct guesses divided by the maximum target. Correct Guesses / s is my hash rate multiplied by the Chance to Guess. The Time to Guess is one divided by the correct guesses per second.
These were my theories for the behavior of my proof-of-work script.
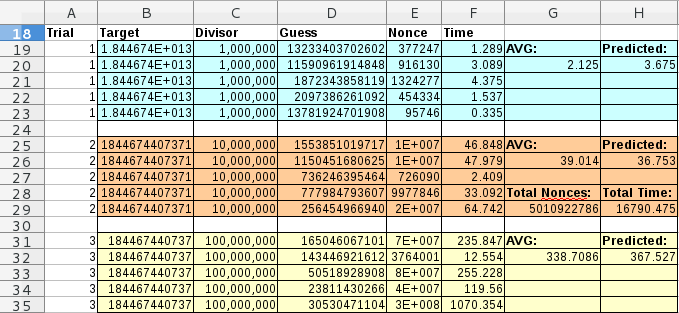
I ran multiple timed experiments; the results are shown here:
You can see how the nonce and time scale linearly. The Guess is the actual value of the correct guess. E.g. Guess is decimal representation of the first 8 bytes from the double SHA256 hashing of the payload and Nonce.
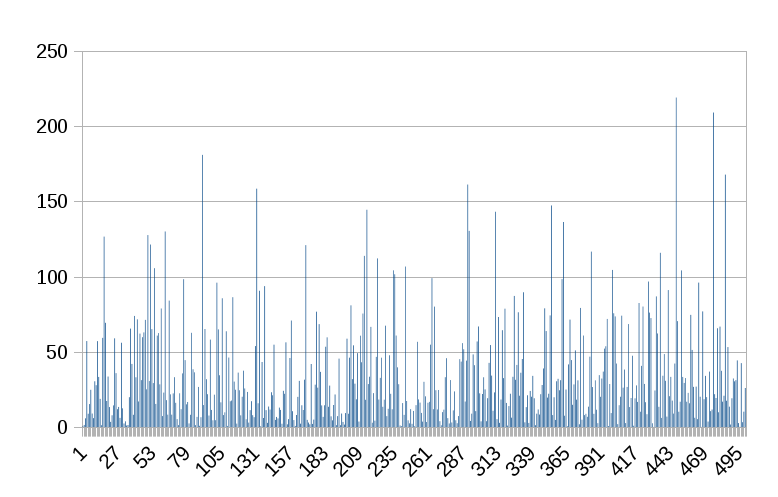
Five trials were run for each difficulty. For such a miniscule sampling, I wasn’t too far off from my predictions and real life will never mirror theory. I decided to run 500 trials for the middle row, difficulty 10,000,000. It ran for around four and a half hours. The Total Nonces, Total Time column displays the aggregates for the run of 500. Below is a graph of each guess – or my computer mining on this script.
All of the above code, data can be found on github .
What do you think about Proof-of-Work? Comment Below
Images from Shutterstock.